Nishant Chandgotia
Reader (F)
Website
Tilings in Zd
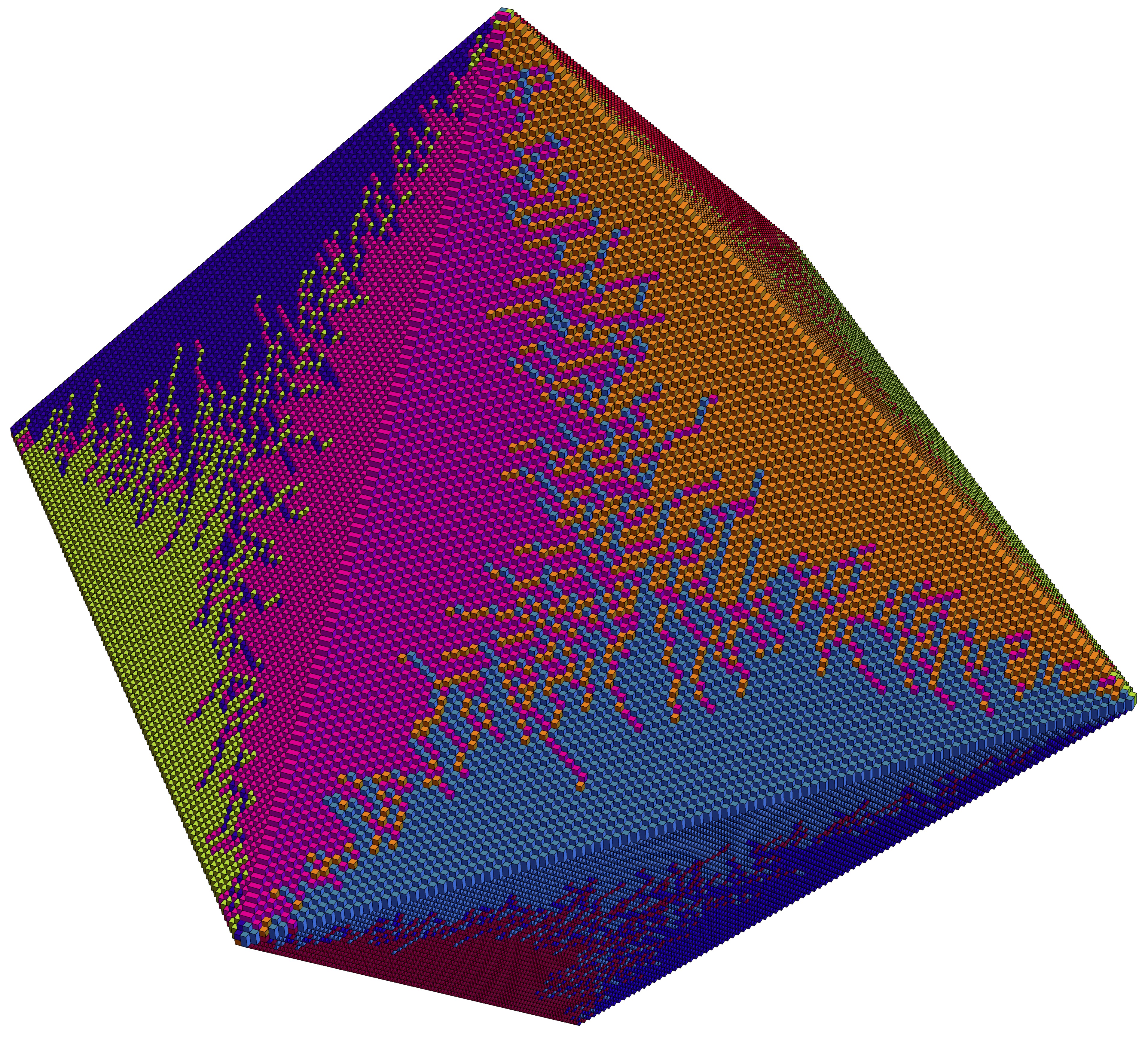
My broad research interests lie in combinatorics, ergodic theory and probability. Let me discuss a specific line of research which has intrigued me off-late. We have all played with puzzles where one is given a set of tiles and has to figure out what shapes can be made using them. This turns out to be a difficult question in general and depending on the set of tiles is related to interesting questions from analysis, geometry and combinatorial group theory. I am interested in simple cases of such questions where these tiles are rectangular boxes of integer lengths and the vertices of these boxes fall on the vertices of Zd. There are several related questions which arise: Suppose a shape can be tiled by a given set of tiles. Can we describe what a random tiling looks like? Is there a nice algorithm which can determine a tiling? Can you move from one tiling to another using some local moves? More details can be found in https://nishantchandgotia.github.io/Research.html
A random tiling of an Aztec octahedron by Scott Sheffield and Catherine Wolfram, see https://arxiv.org/abs/2304.0846