Atul Shekhar
Reader (F)
Schramm-Loewner-Evolutions and related random geometrical objects
I am a probabilist working in the broad area of Random geometry. Nowadays, various random geometrical objects have emerged as objects of substantial importance describing the microscopic behaviour of many physical phenomenas. Let me use an example to explain it well. Consider the study of magnetic properties of a material. When a piece of magnet is heated, at a certain temperature called the Curie temperature, the magnet loses its magnetic property. Physicists Wilhelm Lenz and Ernst Ising proposed a model now known as the Ising model to describe this phenomenon. Atoms of the material form a lattice structure, and each site of lattice has +1 or -1 spin which are randomly assigned according to certain probabilities. The magnetic property is a result of how these spins interact with each other. At the Curie temperature, these interactions undergo a phase transition whose physical manifestation is the loss of the magnetic property. To study the magnetic properties of the given material at the Curie temperature, it becomes necessary to study the corresponding spin profiles. This in turn can be studied by studying the interface separating the +1 spins from -1 spins. These interfaces satisfy a curious property of conformal invariance which means that its properties remain invariant rotation, translation and dilatation. Before 1998, people had no idea how to mathematically describe these interfaces. But then a breakthrough was made by Oded Schramm who introduced the Schramm-Loewner-Evolutions (SLEs) which are the random geometrical objects describing these interfaces. The construction of SLEs itself is a beautiful elegant mixture of probability theory and complex analysis. SLEs has ever since been a very active field of research, so much so that this field of research has won many Fields medals (Wendelin Werner, Stanislav Smirnov, Hugo-Duminil Copin. Wendelin Werner was the first probabilist to be ever awarded a Fields medal and since then people have realised that probability theory is an important indispensable field of mathematics, and it is not just a part of applied mathematics). The SLEs are also connected to other random geometrical objects such as Gaussian Free Field and Liouville Quantum Gravity (LQG). These random objects also arise in mathematical physics, particularly in quantum field theory. Studying the interplay between SLE, GFF, LQG is currently a very active field of research.
My field of research is in understanding different analytical and geometrical aspects of SLEs/GFFs. You can find my papers here: https://arxiv.org/search/math?searchtype=author&query=Shekhar,+A
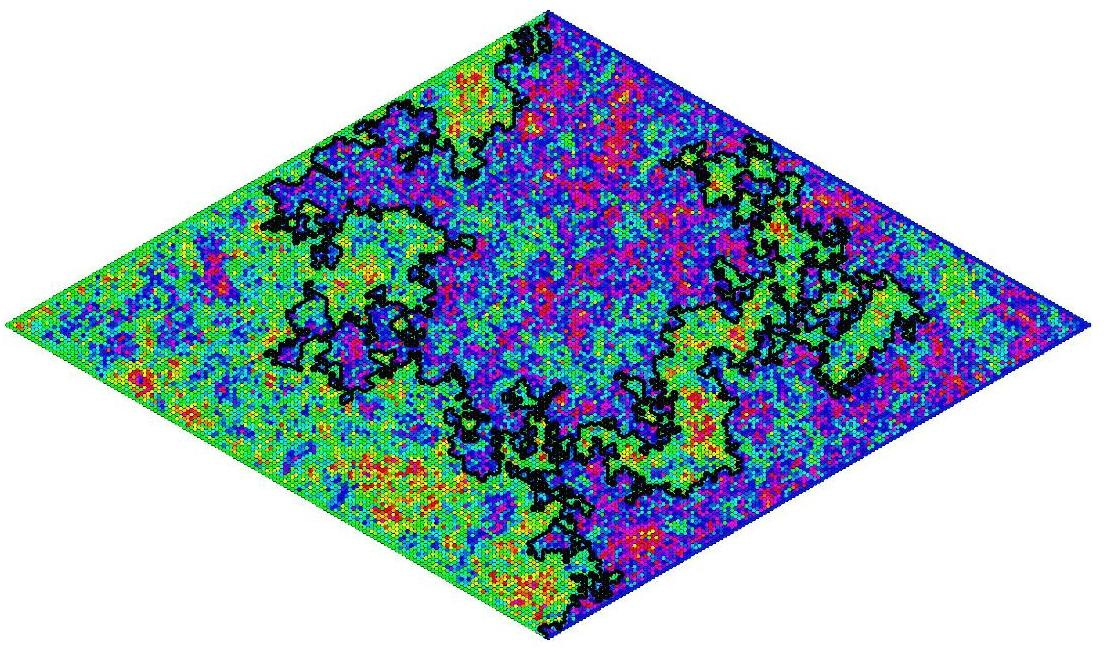
Coupling of SLE and GFF (Picture courtesy Scott Sheffield)
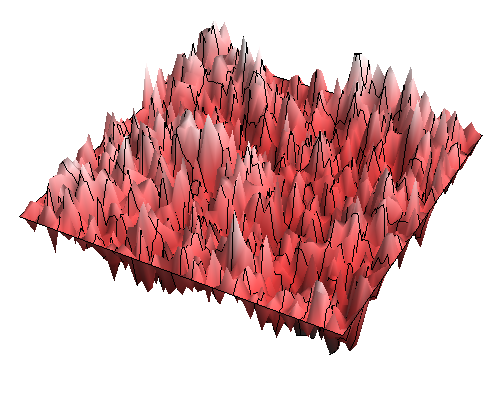
Gaussian Free Field (Courtesy Wikipedia)
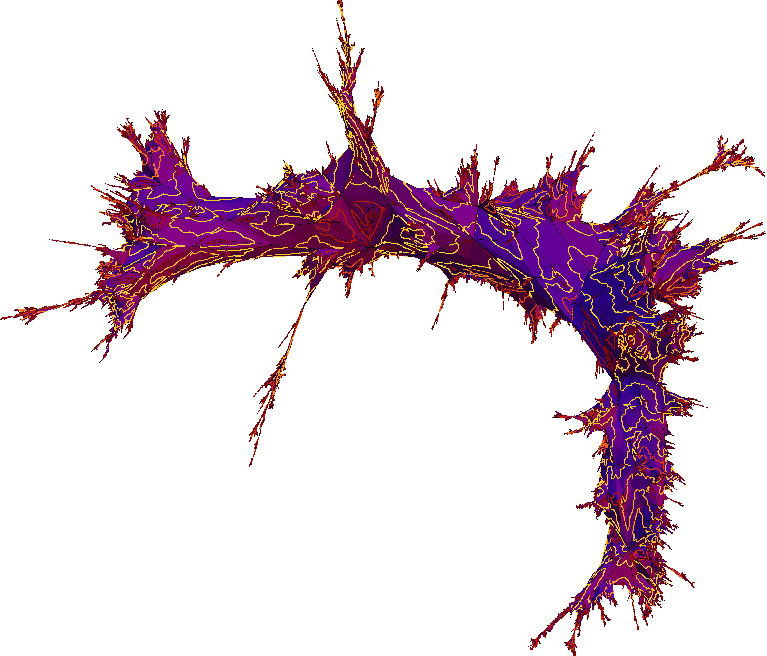
Liouville Quantum Gravity (Picture courtesy J. Bettinelli and B. Laslier.)